
PROTON MONTE CARLO DOSE CALCULATION IN RAYSTATION
RayStation 6 introduces a Monte Carlo (MC) dose engine for proton pencil beam scanning (PBS) plans, which can be used in parallel with the existing pencil beam dose engine. Both dose engines can be used in the same way, so it is possible to compute spot dose distributions as input for optimization as well as to compute the dose for an existing proton PBS plan. Dose can also be computed for beams holding beam modifiers, such as range shifters and patientspecific aperture blocks with arbitrary air gaps. As with the pencil beam dose engine, the aperture block can also be included during the optimization.
The algorithms and their implementation in the MC dose engine are specifically geared to meeting the accuracy requirements of dose calculation for treatment planning. The goal is to optimize speed while maintaining accurate modeling of the relevant physics processes.
In RayStation, a single PBS machine model for a particular delivery system can support both the MC and the PB dose calculations. The beam-measurement data needed for commissioning is the same for both dose engines.
TRANSPORT MECHANISMS
The Monte Carlo code transports primary protons and secondary ions (protons, deuterons and alphas). A Class II transport method is applied for the primary and secondary protons, while the heavier secondaries are transported only accounting for energy loss in a continuous slowing down approximation (CSDA). Nuclear absorption is thus neglected for the secondary deuterons and alphas.
Neutral reaction products (neutrons and gammas) are not transported, but their given fractions of the absorbed energy are included in the energy balance and considered to leak out. Delta electron production is not considered. This is justified by the fact that released electrons have on average a very short range and are therefore not relevant for the calculation of physical dose in voxels of size 1 mm or larger. For example, for a 200 MeV proton, the highest delta electron energy is around 500 keV, which corresponds to a range of approximately 2 mm in water. With a cross-section that is strongly peaked towards lower energies, the net inter-voxel effect becomes negligible.
The MC dose engine reports physical dose as dose to a small water cavity embedded in the local medium, i.e., as dose-to-water in agreement with the PB dose engine. The transport simulation is performed in geometries represented by rectilinear voxel grids where a voxel is characterized by its mass density, elemental composition and mean ionization energy.
For a patient, the transport grid coincides with the dose reporting grid. Beam modifiers are represented by rectilinear grids where the grid dimensions are chosen such as to best represent each beam modifier.
BEAM MODIFIERS
For the beam modifiers, one of the cardinal directions of the transport grid is aligned with the beam’s central axis during the transport simulation. The gaps between transport grids (e.g. the air gap between a range shifter and the patient) is treated as vacuum. The transport simulation in beam modifiers is carried out using the same transport mechanics and physics models as for patients, the difference being that energy depositions are only scored while in the patient transport grid.
The Monte Carlo transport starts by generating primary protons in a plane upstream of the patient transport grid, or upstream of the furthest upstream beam modifier if present. The protons are then propagated through the transport grids until they either stop or escape from the geometry. The MC and PB dose engines use the same parametrization of the incident phase space per spot.
ELECTROMAGNETIC PROCESSES
In both the MC and the PB dose engines, the calculation of proton stopping power uses the same models for ionization energy loss and material modeling. But to increase performance in the MC dose engine, the ionization energy loss integration is carried out using a parametrized model of the Bethe-Block equation. Energyloss straggling is handled by the Bohr approximation. Modeling of multiple scattering uses the theory of Goudsmit-Saunderson.
The transport mechanics, i.e., the method of propagating ions through the scoring grids and the incorporation of the electromagnetic processes (ionization energy loss, energy loss straggling and multiple scattering), are deeply intertwined. Thus, the transport mechanics uses the random hinge method pioneered in MC codes for electron/positron transport. In the current implementation, a sequence of random hinges, where each hinge may extend over multiple voxels, is applied until the ion energy reaches an energy threshold.
While energy loss and nuclear absorption must be computed for every voxel traversal, multiple scattering and energy straggling are only computed once per random hinge, enabling an efficient calculation scheme.
The modeling of non-elastic nuclear reactions is data driven and based on a cross-section data library derived from published ICRU63 data. No models are used. Elastic scattering of protons on hydrogen and on nuclei are included through parametrized models of the absorption probabilities and angular differential cross-sections.
FINAL DOSE CALCULATION
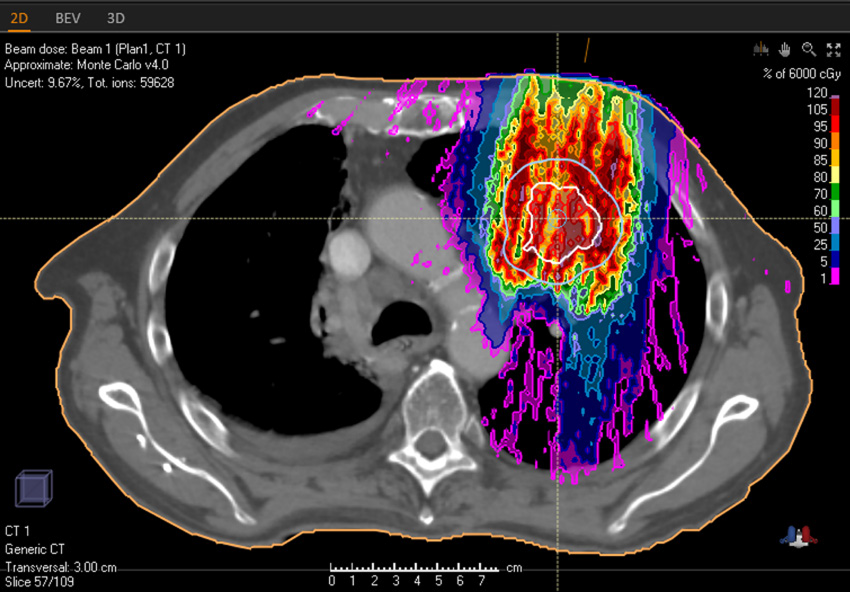
For final dose calculation in a PBS treatment plan, statistical error is estimated using the method of independent batches. The statistical error per voxel is estimated as the dose variance of the dose per voxel across all batches (12 batches are currently used). A single statistical error estimate is reported per beam as the mean one standard deviation error across all voxels with a dose above 50% of the maximum dose per beam.
The MC calculated final dose will be marked as clinical if the statistical error per beam is smaller than a user-defined threshold. Otherwise, the dose will be considered as approximate. The statistical error is not calculated when the MC dose engine is used to drive the optimization. The dose after optimization will therefore always be considered as approximate when the MC dose engine is selected for optimization. The calculation is deterministic, i.e., repeated calculations yield the same numerical result.
CONCLUSION
The MC dose engine in RayStation 6 adds an additional dimension of precision to proton PBS planning. It strikes the optimal balance between accurate physics modeling and speed, making it highly effective in clinical workflows. The MC and PB dose engines are designed to be used in parallel, ensuring efficient and accurate dose calculation for all proton PBS planning needs.
For more information or to see a demo, contact sales@raysearchlabs.com